素粒子物理学Iレポート　No.3(改訂版)（提出期限　5月28日）

1. Dirac方程式の解に対して, を示す。

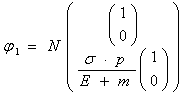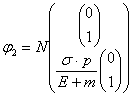1.1　、を用い

となることを示せ。も求めよ。

1.2　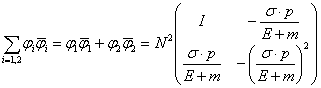となることを示せ。

1.3　となることを示せ。（ヒント）スピン演算子の性質とを使えば自明。

1.4 と規格定数を選び1.2問のを更に計算する。

（注）Nは1.3問より単位体積中に２E個の粒子があるように規格化する。もし単位体積中に１個の粒子で規格化するとローレンツ収縮で体積が変化したときに確率密度を不変にできないので、相対論では単位体積中に２E個の粒子という共変的規格化を選ぶ。

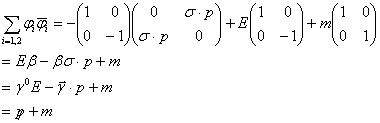
となることを示せ。ただし、である。

1.5　同様にとなることを示せ。

2. 意欲のある人は式(2.18)のを正確に書いたときに

となることを示せ（採点には加えないので、意欲のある人が自主的にやるだけでいいです）。

3. マンデルシュータム変数の関係式を示しなさい。また、p_a®−p_dの置き換えでマンデルシュータム変数sとtが入れ代わることを示せ。

4. (2.25)について重心系で粒子の質量が無視できる場合、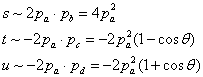

となることを示しなさい。ただし、θは重心系での散乱角である。

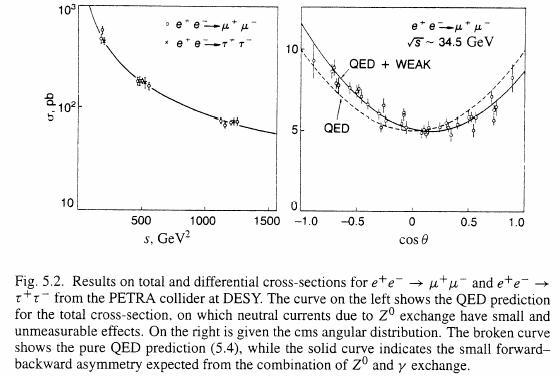
5. 現在日本のBファクトリー実験は重心系エネルギー10GeVでBB(―)中間子を大量生成し実験を行っている。は何pbか？pbは10^-12×b(10^-24cm²)=10^-36cm²である。また現在Bファクトリーは10³⁴cm^-2s^-1という高ルミノシーティーで実験を行っている。毎秒何個のm⁺m^-対が生成されているか？

参考資料