素粒子物理学Iレポート　No.2（提出期限　5月7日）

1. 電子ニュートリノ、ミューオンニュートリノは質量の異なるニュートリノn₁、n₂の混合状態として、

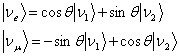
と表せる。の時間発展は　、

と表せる。時刻t=0で純粋にの状態のニュートリノがｔ秒後にが出現する確率を求めたい。

1.1　を、の状態で表せ。

1.2　出現の確率が

---- (1)

と表せることを示せ。

1.3　ニュートリノが光速で走るとして、上記の式でm₁(eV)、ct=L[km]、p=E[GeV]の単位系で式（１）を表現するとき

となる係数αを求めよ。（ヒント：上記はニュートリノ振動の基本的な式で、素粒子の教科書を探せば導出は載っているものもある。）

2. Dirac方程式においてψの4成分を別々にして、それぞれの成分ψ₁、ψ₂、ψ₃、ψ₄で４つの方程式をあらわに書き出せ。

3. γ行列の公式 、γ^0†＝γ⁰、(γ⁰)²＝I、γ^k†＝(ba^k)^†= a^kb=-γ^k、(γ^k)²＝-Iを示せ。またエルミート共役の結果はγ^m†＝γ⁰γ^mγ⁰を示せ。

4. 式(2.7)に続きψ₃、ψ₄を求めよ。ここでvは負エネルギー解よりE-mのEは負エネルギーで、正エネルギーE®-|E|と変換するとE-m=−（|E|＋ｍ）と表せる。

5. 4成分ヘリシティ演算子がディラックハミルトニアンと交換することを示せ。よってヘリシティはエネルギーと独立な観測可能量であり系を記述するよい粒子数である。

6. が確率密度となることを示せ。