2. 量子電磁力学
2.1 Klein-Gordon方程式と反粒子
相対論的波動方程式を導こう。
E2=p2+m2の式を
![]() ,
, ![]() の関係式を使って演算子に置き換えると
の関係式を使って演算子に置き換えると
![]() ―――(2.1)
―――(2.1)
が得られる。これをKlein-Gordon方程式(相対論的なシュレディンガー方程式)という。
この方程式を満たす、エネルギーE、運動量pの自由粒子の解は
![]() ――― (2.2)
――― (2.2)
である。エネルギー固有値は
![]()
となり、負エネルギーの解が表れた。負エネルギーの解、つまり負のエネルギーの粒子はどんどん低いエネルギー状態に遷移が可能であり、安定した状態を取ることはできない。この状態を歴史的にどう議論してきたかは興味あることである。
例; Diracの空孔理論:Dirac方程式に従う電子を例にとったとき、真空は全て負エネルギーの電子で満たされるとした。
この話題は、あとは教科書に譲ることにする。
式(2.2)で負エネルギーの粒子は、時間を逆向きにとれば正エネルギーの粒子の運動ととれる。つまり
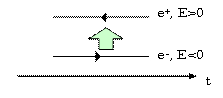
と解釈しなおす。例えば、電子の流れ(電流を)考えると、負電子が右向きに流れていることは、正電子が左向きに流れていることになる。よって、負エネルギーの解は正エネルギーの反粒子として意味を持つことがわかる。同様に反粒子の運動量は![]() となる。
となる。
ここで粒子→反粒子として、正エネルギーを定義できたので、粒子の安定性の問題は避けられた。また、相対論的方程式より、反粒子が存在する示唆が与えられた。
2.2 Dirac方程式
歴史的には2.1の解釈の前に、Klein-Gordon方程式に伴う負の確率(ここでは飛ばした)と負のエネルギーの問題を避けるために、Diracは時間に対して一階の微分方程式を提案した。なぜなら連続の方程式
![]()
におおて、Klein-Gordon方程式では時間の1階微分が初期条件によってしまうのでうれしくない(歴史的には確率密度に電荷eを与え、電子の電荷電流密度として解釈しなおしてこの困難を避けた)。ただし、空間微分の回数を減らしたため、φは多成分となる(例:長島さん教科書p39)。一階の微分方程式は
![]() ――― (2.3)
――― (2.3)
(注:ここでψは多成分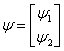 のような列ベクトルとする。成分は2とは限らない)
のような列ベクトルとする。成分は2とは限らない)
この式をKlein-Gordon方程式と比較する。
![]()
この式を解くと
ai2=b2=1
![]()
の関係式が導かれる。この関係式を満たす行列をディラック行列と呼ぶ。
最低次元のディラック行列は4次元(長島教科書p40)であり、4つの行列はDirac-Pauli表現で
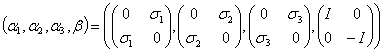 ―――(2.4)
―――(2.4)
でsiはパウリ行列で
![]()
![]()
![]()
である。
式(2.3)に左からβをかけて、Diracのγ行列![]() を導入すると式(2.3)は
を導入すると式(2.3)は
![]() ――――(2.5)
――――(2.5)
と簡単にかける。この方程式は4つ(4連)の微分方程式である。
つまりディラック方程式には4つの解が存在することになる。
[HW] ψの4成分を別々にして、それぞれの成分ψ1、ψ2、ψ3、ψ4が満たす方程式をあらわに書き出せ。
[HW]γ行列の公式
![]() 、
、![]() γ0†=γ0、(γ0)2=I、γk†=(bak)†= akb=-γk、(γk)2=-Iを示せ。またエルミート共役の結果はγm†=γ0γmγ0と書けることも示せ。
γ0†=γ0、(γ0)2=I、γk†=(bak)†= akb=-γk、(γk)2=-Iを示せ。またエルミート共役の結果はγm†=γ0γmγ0と書けることも示せ。
Klein-Gordon方程式のところで、粒子・反粒子二つの解が現れることを確認したが、Dirac方程式では4つ(2倍)になった。この2倍は粒子のどのような状態に対応しているかこれから見ていく。
Dirac方程式は基本的に2行2列のパウリ行列をもとにする4行4列の行列で表されているので、式(2.3)と式(2.4)をもとにψを2次元の列ベクトルu,vを使って![]() とすると、
とすると、
![]() Þ
Þ ![]() ――― (2.6)
――― (2.6)
と表せる。
静止した粒子(p=0)を考えると、Eu=mu, Ev=-mvとなるので、uの状態が正のエネルギーをもつ粒子を、vの状態が負のエネルギーを持つ粒子(つまり反粒子)を表していることがわかる。ここでu、vが2次元の列ベクトルであることを思い出して、それぞれの状態が何に対応しているかを考える。賢明な学生ならパウリ行列σがある時点で、u,vの2成分がスピンに関係しているだろうという推測ができると思う。
式(2.6)下に置いて、ψ1、ψ2のu成分がスピン関数![]() とすると
とすると
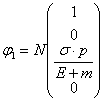 ,
, 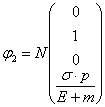 (注:Nは規格化定数)-----(2.7)
(注:Nは規格化定数)-----(2.7)
と表せる。ここで、非相対論の場合を考えると、|E|-m, |p|<<|E|, mなので正エネルギーの場合はu>>vである。
同様に式(2.6)上を用いて、ψ3、ψ4を求めることができる。
[HW] ψ3、ψ4を求めよ。ここでvは負エネルギー解よりE-mのEは負エネルギーで、正エネルギーE®-|E|と変換するとE-m=−(|E|+m)と表せる。
よって4つの解が得られたことになる。ψ1、ψ2は正エネルギーに、ψ3、ψ4は負エネルギーに対応する。
2.2.1 ヘリシティー
上記(2.7)の式で、運動量p=0、E=mの場合の波動関数は
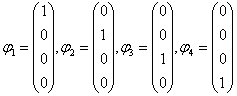
であり、2次元のスピン演算子![]() を4次元に拡張した
を4次元に拡張した
![]() のΣ3は上記波動関数を固有関数としてもっている(固有値は±1/2)。
のΣ3は上記波動関数を固有関数としてもっている(固有値は±1/2)。
スピン角運動量はよく粒子の自転の角運動量に例えられるが、回転という概念は広がりを持った質量分布が必要である。スピン角運動量は広がりのない質点粒子でも相対論的取り扱いから必然的に出てくる量であり、座標や運動量といった変数を含まない。相対論的粒子に付随する一つの性質として受け入れるべきである。
相対論的取り扱いでは固定したz軸の代わりに、自身の運動方向をz軸にとった場合のスピンのz成分(ヘリシティ)がよく使われる。ヘリシティhは
![]() ―――――(2.8)
―――――(2.8)
で定義され、±1の固有値を持つ。ヘリシティ正は右方向に回転して進む右巻きねじに対応させる。このため、ヘリシティは正負の代わりに右巻き、左巻きという表現をよく使う。
[HW]4成分ヘリシティ演算子がディラックハミルトニアンと交換することを示せ。よってヘリシティはエネルギーと独立な観測可能量であり系を記述するよい粒子数である。
(注)軌道角運動量L=r×pとハミルトニアンの交換関係は[H,L]=-i(a×p)である(注:αは(2.4))。全角運動量![]() はHと可換であり、保存するよい量子数である。
はHと可換であり、保存するよい量子数である。
[HW]参考として、長島教科書p57~p61、もしくはクォークとレプトンのp121~123を読んでみて下さい。理解できなくても、頭のすみに止めておくと、そのうちニュートリノの話が出てきたときに少し理解が深まるかもしれません。
2.2.2 Dirac粒子の磁気能率
ディラック方程式に従う粒子と電磁場の相互作用を考える。シュレディンガー方程式の場合と同様に
![]() もしくは(
もしくは(![]() )
)
として電子の場合(q=-e)から式(2.6)より
![]() ―――――(2.9)
―――――(2.9)
E>0の解
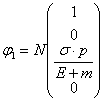
で非相対論的近似を行うと
![]()
これを(2.9)上式に代入すると(E=m+T, T<<m, eφ<<mと仮定)
![]()
ここでスピン演算子の性質![]() を使い、公
を使い、公![]() を使って式を整理すると
を使って式を整理すると
![]() ―――――(2.10)
―――――(2.10)
となる。この式は電子と磁場の相互作用が含まれている。磁気能率μと磁場Bの相互作用![]() を思い出すと、電子の磁気能率は
を思い出すと、電子の磁気能率は
![]()
と書け、gをg因子(g factor)とよびg=2である。
電子の磁気能率はg因子2を持つ。g因子は通常非常に2に近く、Dirac方程式の予言が実証されたことになる。実験ではg因子の2からの差(g-2)を異常磁気能率と定義し測定している。陽子の磁気能率を測定するとg=2.79となり、基本粒子でないことがわかる。また中性子も磁気能率g=-1.91をもち基本粒子でないことがわかる。中性子は電荷を持たないのに磁気能率を有している。これはまさに中性子に構造(もしくは有限の大きさ)があることを示唆している。
2.2.3 保存カレント
Dirac方程式のエルミート共役(行列なので、複素共役ではない)をとると
![]()
ここでγ行列のエルミート共役![]() は0成分と1-3成分で変換性が異なる。共変型を保つために
は0成分と1-3成分で変換性が異なる。共変型を保つために![]() を定義し、常識の右から
を定義し、常識の右から![]() をかけると
をかけると
![]() ―――――― (2.11)
―――――― (2.11)
が導ける。Dirac方程式(2.5)と共変型(2.11)を使って連続の方程式
![]() が導ける。
が導ける。
よって![]() は連続の方程式
は連続の方程式![]() を満たすjm(カレント)となっている。
を満たすjm(カレント)となっている。
[HW] ![]() が確率密度
が確率密度![]() となることを示せ。
となることを示せ。
2.2.4 反粒子状態(荷電共役変換)
荷電共役変換とは粒子と反粒子とを入れ替える演算である。粒子と反粒子の違いは電荷にある。荷電共役変換(ψ®ψc)を施したDirac方程式の波動関数(ψc)はディラック行列を使って
![]()
と表せる(長島教科書56ページもしくはクォークとレプトン116ページ参照)。
2.3
相対論的反応断面積
2.3.1 電磁場AmによるDirac粒子の散乱
Dirac方程式(2.5)に電磁場がある場合の方程式は![]() として
として
![]() ――――(2.12)
――――(2.12)
この式を1次の摂動で取り扱う{注:(E+∙∙∙)ψ=Vψの形でVを定義}。摂動による状態の時間変化を考える場合、状態ψiから状態ψfへの遷移振幅Sfiは![]() をとq=-e(電子の場合)を用いて
をとq=-e(電子の場合)を用いて
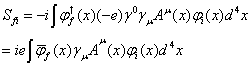
2.23節でやったように![]() は連続の方程式
は連続の方程式![]() を満たすカレントと考えられたので、
を満たすカレントと考えられたので、![]() をカレント(電流?)と定義すると
をカレント(電流?)と定義すると
![]() ――――(2.13)
――――(2.13)
と書ける。この反応を図式すると
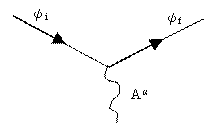
となる。
2.3.2 カレントの表式
Dirac方程式の時間発展する解は
![]()
と書けるので、入射粒子の4元運動量をpi、終状態の粒子の運動量をpfとすると
![]() ――――(2.14)
――――(2.14)
とかける。ここでuは式(2.7)のように4次元のスピノールである。
2.3.3 電磁場のAmの表式
電磁場Aμも通常荷電粒子によって生成されている。ここで電磁場Aμが電子によって生成されるとし、その電子の始状態の運動量をp1、終状態の粒子の運動量をp2とすると、そのカレントは
![]() ――――(2.15)
――――(2.15)
と表せる。このカレントがMaxwell方程式を満たす条件より
![]() ――――(2.16)
――――(2.16)
となる。式(2.15)を式(2.16)に代入しq=( p2 −p1)とすると式(2.16)は
![]() ――――(2.17)
――――(2.17)
となる。
2.3.4 Dirac粒子同士の散乱−1(Trace公式)
ここで全ての道具立てが揃ったので、Dirac粒子同士の散乱を計算する。実際にはミューオンが入射して電子(標的)により散乱される過程を計算する。入射粒子と標的粒子が同じ(電子電子散乱)場合は、最終的に観測される電子が入射粒子だったのか、標的粒子だったのかを識別することが不可能になり、その分計算過程が増えるので、ここでは異種粒子同士の散乱をj考える。散乱の様子をファインマンダイアグラムで表すと、
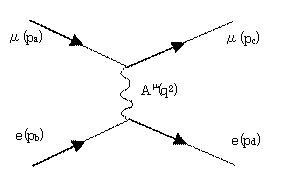
である。この反応の散乱振幅は式(2.13)、(2.14)、(2.17)より
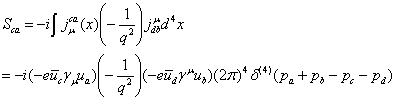
となる。ここでδ関数の意味は4元運動量移行の保存である。
ここで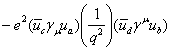 を不変振幅Mと定義する。
を不変振幅Mと定義する。
散乱断面積は散乱振幅の2乗よりM2を計算する必要がある。
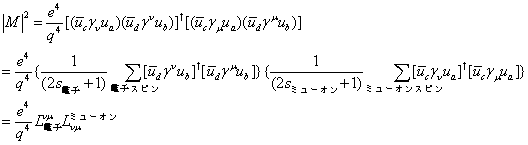
となる。ここで1/(2s+1)の因子は粒子の始状態のスピンがわからないので、全スピン状態について平均を取ってあり、Σスピンは終状態が全てのスピン状態を含むので和をとっている。
この![]() を計算する必要がある。
を計算する必要がある。
ここでエルミート共役の括弧は
![]()
となり、エルミート共役は単に粒子bとdの順序を入れ替えただけである。各行列の成分をあらわに示すと
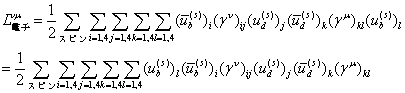
![]() より
より
[HW] ![]() ,
, ![]() を示せ。
を示せ。
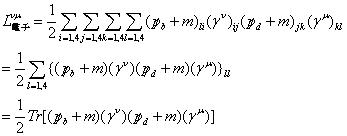
となる。
(付録)トレース定理とγ行列の性質(クォークとレプトンp130)
![]()
ここで、mの1次の項は奇数個のγ行列を含んでいるので0.
![]()
![]()
![]()
2.3.5 Dirac粒子同士の散乱−2(散乱断面積)
電子の質量をmeミューオンの質量をmmとすると、
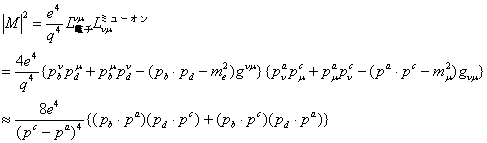 ――(2.18)
――(2.18)
ここで最後の式変形で、高エネルギー反応を扱うという仮定のもと、粒子の質量を無視した。
[HW] 意欲のある人は式(2.18)の![]() を正確に書いたときに
を正確に書いたときに
![]()
となることを示せ。
微分断面積は、入射粒子のフラックスをF、終状態の数をdLips(ローレンツ不変な位相空間因子)として
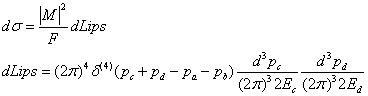
として表せる。
重心系での断面積。E+eàmumuの断面積。Mandelstam変数。