�P�D���_
�{�u�`�͍��G�l���M�[�����w�i�f���q���������w�j�̊ϓ_����A�f���q�����w�̊T�v���u�`���܂��B����͏�̗��_�̊ϓ_����A�f���q�����w�ɂ��ču�`�����ł��傤�B
1.1�@�f���q�Ƃ�
�@���E���\������ŏ��̊�{�P�ʁB�܂萢�E�͉�����ł��Ă��邩�Ƃ����A�f�p�ȋ^��ɓ�����w�₪�f���q�����w�ł��B
�@�f���q�����ƌ��q�E���q�j�����̈Ⴂ�͂Ȃ�ł��傤�H
�@���ʓ_�F�@�Ƃ��ɏ����Ȑ��E�������Ă���i�ʎq�͊w�j�B
Þ�@�����́��d�����ݍ�p�E�������ݍ�p�E�ア���ݍ�p
�@�قȂ�_�F
�f���q�����@Þ�@�f���q�͐��E�̊�{�\���v�f�B
��{���q�i�����\���������Ȃ����_�j�̐����Ƃ��̉^���ׂ�
��1�������畨����T������BSimple is Best�B
���q�E���q�j�����w�@Þ�@���������w�Ɠ����Łi�L���j���̌n�ł���B
���ۂ����܂��������郂�f���\�z��ڎw���B
����āA��{�I�ɂ͂��Ȃ�قȂ����w��ł���A�f���q�����w�͕����̒��ł����قȕ���ƌ�����B�@
�f���q�Ƃ�
�@�N�H�[�N�ƃ��v�g���i�������\�����闱�q�j�F�t�F���~�I���@�X�s��1/2
|
|
��1���� |
��2���� |
��3���� |
|
�N�H�[�N |
u-quark (up) |
c-quark (chram) |
t-quark (top) |
|
d-quark (down) |
s-quark (strange) |
b-quark (bottom) |
|
|
���v�g�� |
e�i�d�q�j |
m(�~���[�I��) |
t(�^�E) |
|
ne(�d�q�j���[�g���m) |
nm(�~���[�I���j���[�g���m) |
nt(�^�E�j���[�g���m) |
�{���̔����q
�A�Q�[�W�{�]���i�͂�`���闱�q�j�F�@�x�N�^�[�{�\���@�X�s���P
|
�d���� |
g (���q) |
�d�� |
|
�ア�� |
W+, W-, Z+0 |
��d�� |
|
������ |
g(�O���[�I��):8��ށFg(RR), g(RG), , g(RB), g(GR), g(GG), g(GB), g(BR), g(BG), g(BB)-[ g(RR)+ g(GG)+ g(BB)] |
�J���[�ׁiR,G,B�j �d�ׁF�{�A�|�̂悤�Ȃ��� |
�B�q�b�O�X���q�F�@�X�J���[�{�\���@�X�s���O
H�@�i1�ȏ�j�G�@�e�f���q�Ɏ��ʂ�^���闱�q�B
�mHW�n�e�f���q�̎��ʂƎ����ׂȂ����i���m�Ȓl�Ŗ����A��̂̃X�P�[���ł悢�B��`���[���N�H�[�N~1.4GeV�A����10-13~10-12s�j�B��������`�ł��Ȃ��ꍇ�́A���q�̕��������Ȃ����B�i��FW�{�\���A����2.118 GeV�j�܂��e�f���q�ɓ����͂̎�ނ��Ȃ����B
�������ݍ�p�̍u�`���ɐ������܂����A�N�H�[�N�ƃO���[�I���͒��ڊϑ�����܂���B�ϑ��ɂ����闱�q��
�@�o���I���i�j�q�̒��ԁj
�@p(�z�q)[uud]�An(�����q)[udd]�A���{�{�i�f���^�j[uuu]�A���i�����_�j[uds]�A
���{(�V�O�})[ uus]�A��0�i�O�U�C�j[uss]�A��-�i�I���K�j[sss]�A��c+�i�����_�j[udc]�c
�A���\��
�@��+�i�Β��Ԏq�j[ud]�A��0�i�G�[�^���Ԏq�j[ud+ud+ud]�A�ρi�ϒ��Ԏq�j�A�ցA�Ӂi�Ӓ��Ԏq�j[ss]�AK�{�iK���Ԏq�j[us]�AK0�iK���Ԏq�j[ds]�AJ/�Ձi�W�F�[�E�v�T�C�j[cc]�AD�{�iD���Ԏq�j[cd]�A���i�E�v�V�����j[bb]�AB�{�iB���Ԏq�j[ub]�ABC�{[cb]�c
�@�Ɩ����ɑ��݂���B�f���q�ł͂Ȃ����A�����A�f���q�����Ŏ���ƂȂ�̂̓��v�g���������͏�L�̗��q�i�f���q�ł͂Ȃ��j�ł���B
1.2�@��
�f���q�ɓ����͂́A�d�́E�d���́E�����́E�ア�͂�4��ނł��邪�A�d�͔͂��ɏ������̂ŁA�����ł͎�舵��Ȃ��B
Ø �d���� �ie+��e-�j
Ø
�d�� ![]()
Ø �ア�� �in��e, m�j
Ø ������ �in«p�j
|
�� |
���� |
���B���� |
���� |
|
������ |
1 |
10-15m |
�z�q�A���q�j�𑩂˂�� |
|
�d���� |
0.01 |
�� |
�g�̉��̏d�͈ȊO�̗́B�d�C�B���݂Ȃ�B���q�ԗ́B |
|
�ア�� |
0.00001 |
10-17m |
�x�[�^����A�j���[�g���m�A���z�̔R�� |
|
�d�� |
10-38 |
�� |
���L���́A�F���̌`�� |
�ア�͂Ƌ����͂͒Z�����͂Ȃ̂ŁA��X�̓��퐶���ŗ͂������邱�Ƃ͂Ȃ��B�������A��X�̐��E���`�������ł͕K�v�s���ȗ͂ł���B
[HW] �Ȃ��A�ア�͂Ƌ����͂��Z�����͂Ȃ̂����ׂĂ݂ĉ������B���͈͂قȂ������R�ɂ��Z�����͂ƂȂ��Ă��܂��B
1.3�@�f���q�����w�̗��j
�z�z�����Q�l�B��100�N�O��J.J. Thomson�ɂ���čŏ��̑f���q�g�d�q�h���������ꂽ�B1920�`1930�N�ɗʎq�͊w���m������A�ߑ�I�ȑf���q�����w��1930�N���̗z�q�A�����q�̔����ADirac�������̊m������X�^�[�g�����Ƃ�����B1960�`1970�N��̃N�H�[�N�͌^�A�e��f���q�̔����A�d�㓝�ꗝ�_�A1980�`1990�N��̃Q�[�W�{�\���̌����A1990�N��̏��сE�v��s��̊m���A1998�N�j���[�g���m�U�������ɂ��W�����_���z�������ۂ̔����Ƒ����Ă���B
1.4���R�P�ʌn
��{�P�ʌn�i�l�j�r�P�ʌn�G�l[���[�g��]�A�j[�L���O����]�A�r[�b]�A�`[�A���y�A]�j�̓}�N���Ȑ��E���L�q����̂ɓK���Ă��邪�~�N���Ȑ��E��\���ɂ͕s�����ł���B
���R�萔
|
���� |
�L�� |
�l |
�P�� |
|
�v�����N�萔 |
|
1.05457266�L10-34 |
m2kg•s-1=J•s |
|
���� |
c |
299,792,458 |
m•s-1 |
|
�f�d�� |
e |
1.602217733�L10-19 |
A•s |
|
�d�͒萔 |
G |
6.67259�L10-11 |
m3kg-1•s-2 |
���R�P�ʌn�F h
= c = e0 (�^��̗U�d��)=1 (m0=1�Ƃ��Ȃ�)
![]() �@�@�@ Þ�@e = 0.0917012
�@�@�@ Þ�@e = 0.0917012
![]() �G�l���M�[�F�@1eV=1.602�~10-19J
�G�l���M�[�F�@1eV=1.602�~10-19J
1keV=103eV, 1MeV=106eV, 1GeV=109eV, 1TeV=1012eV
![]() ���ʁF 1eV/c2 = 1.78�~10-36 kg
���ʁF 1eV/c2 = 1.78�~10-36 kg
�d�q��511keV/c2�A�z�q��938MeV/c2
![]() �^���ʁF1eV/c=0.535�~10-27 kgm/s
�^���ʁF1eV/c=0.535�~10-27 kgm/s
![]() �f�ʐρF
�f�ʐρF![]()
![]() (��)���͏d�S�n�̑S�G�l���M�[��2��
(��)���͏d�S�n�̑S�G�l���M�[��2��
���̔����̒f�ʐς�m2�ŕ\���ƁA�G�l���M�[1GeV�ł̔����f�ʐς�
![]()
s~2pr2=9�~10-36
r~10-18m�G�@����Ĕ������q���ÓT�I�ɑ傫��������Ƃ���Ƃ��̑傫����10-18m�ɑΉ�����B���̑Ή��͐��m�ł͂Ȃ��A�F����ɑf���q�����̑傫���̃X�P�[���𗝉����Ă��炢���������ł��B
[HW]�Β��Ԏq�̎��ʂ�140MeV�Ƃ��āA�s�m�萫����![]() �ADl=cDt�A���g���ĉ��z�Β��Ԏq�����ݍ�p���y�ڂ�����
�ADl=cDt�A���g���ĉ��z�Β��Ԏq�����ݍ�p���y�ڂ�����![]() �����߂�B
�����߂�B
1.5�@���Θ_�̊W���ƃ��[�����c�ϊ�
![]() 4���x�N�g��
4���x�N�g��
4�����W �@xº(x0, x1, x2, x3) º (ct,x)�A�@
4���^���� �@pº(p0, p1, p2, p3) º (E/c,p) ���F�P�ʂ����킹��
![]() ����
����
a•bºambmº a0b0 + a1b1 + a2b2 + a3b3º a0 b0�]a•b
�@bmº (b0,-b)
�@p2=(E/c)2-p2=m2c2
![]()
�Θ_�I�Ɍ��imc>>çpç�j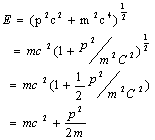
Ø �v�Z��
Z�{�\���i90GeV/c2�j�����ɕK�v�ȉ�����G�l���M�[
² �d�q�E�z�d�q�Փˎ���
p1=(E1/c,p1), p2=(E2/c,p2) p=- p�Ame=511keV/ c2
(E/c+ E/c)2=902/c2
E=45 GeV
² �z�q�Œ�W�I����
p1=(E1/c,p1), p2=(E2/c,0) p1=(0,0,pz)�Ap2=0�Amp~1GeV/ c2
(E1/c+
mp,p1) 2=902/c2
p>>mp���
2 mp E1 =902
�@E1 ~4000GeV
![]() ���[�����c�ϊ�
���[�����c�ϊ�
�����nK�ɑ��āA�������ɑ��xvºbc�œ����Ă���ʂ̊����nK�f�ł̍��W��
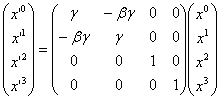 �@�@�\�\�\�\�i1.1�j
�@�@�\�\�\�\�i1.1�j
�ƕ\����B������b�Ag��
![]() �@�@
�@�@![]() �ł���B
�ł���B
[HW] ��(1.1�j�̋t�ϊ������߂�B�܂芵���nK�̍��W�������nK�f�̍��W�ŕ\���B
�܂����q�̃G�l���M�[�Ɖ^���ʂ�
E=gmc2, p=gmbc
�ƕ\����B
[HW]�G�l���M�[10GeV����������500MeV/c2��K�{���Ԏq��b��g�����߂�B����K���Ԏq�̎����i�Î~�n��12nsec�j�͉�nsec�Ɗϑ�����邩�H
1.6�@�s�m�萫�����Ɨ��q�̎���(t): t�b��ɗ��q�̌���1/e�ƂȂ�B
�ʁF2.2��(10-6)sec�A���}�F26n(10-9)sec�A��0�F8.4�~10-17sec(���ڑ���ł�����E)�A
�����q�F886sec
�Z�������q�i10-25�j�F�s�m�萫������藱�q�̎��ʂ̕s�m�萫������B
��E•��t~h (6.5821220�~10-22MeV•s)�A�@
��t~10-25 ��E ~ 6,582MeV (~7GeV)
���������Z�������q�Ɋւ��Ă͗��q���ʂ̕�(G)��1/t�������̑���Ɏg���B