‘fپEٹj¥‰F’ˆژہŒ±ٹw‡TƒŒƒ|پ[ƒgپi‰ً“ڑپj
1.
4Œژ11پC18“ْپ@پ@چ‡Œv”z“_‚Vپi’چپFŒµ–§‚إ‚ح‚ب‚پAگ¬گر‚جژQچlژ‘—؟’ِ“x‚ةژg‚¤پBپj
(ƒA) —zژq‚جڈd‚³‚ح‰½kg‚©پHپ@پi”z“_‚Pپj
1.67262158پL10-27kg.
’تڈي‚ج’Pˆتkg‚إ•\‚·‚ئ‘ه•دڈ¬‚³‚¢‚ج‚إپA‘f—±ژq‚إ‚و‚ژg‚ي‚ê‚é’Pˆت938MeV/c2‚إ•\ژ¦‚·‚éپB
(ƒC) •W“I‚©‚ç10cm‚ج‚ئ‚±‚ë‚ة•\–تگد25cm2‚جNaIƒVƒ“ƒ`ƒŒپ[ƒ^پ[Œںڈoٹي‚ًگف’u‚µ‚½پB•W“I‚ً—ص‚ق—§‘جٹp‚ح‚¢‚‚ç‚©پH‚ـ‚½•W“I‚©‚ç—±ژq‚ھ“™•û“I‚ةژU—گ‚³‚ê‚ؤ‚¢‚é‚ئ‚·‚é‚ئپA‘S‘ج‚ج‰½پ“‚ج—±ژq‚ھŒںڈoٹي‚إٹد‘ھ‚³‚ê‚é‚©پHپi”z“_‚Pپj
•W“I‚ًˆح‚ق‘S—§‘جٹp‚ح4pr2=1257cm2‚ئ‚ب‚éپB‚و‚ء‚ؤNaIƒVƒ“ƒ`ƒŒپ[ƒ^Œںڈoٹي‚ج—ص‚ق—§‘جٹp‚ح25پ€1257پپ0.0199پB•W“I‚©‚ç—±ژq‚ھ“™•û“I‚ةژU—گ‚³‚ê‚ؤ‚¢‚éڈêچ‡‚ح1.99پ“‚جٹm—¦‚إŒںڈoٹي‚إٹد‘ھ‚³‚ê‚éپB
5پ~5cm2’ِ“x‚جNaI‚ح‚و‚‚ ‚é‘ه‚«‚³‚جŒںڈoٹي‚إ‚ ‚éپBگüŒ¹‚©‚ç5cm—£‚µ‚ؤ’u‚¯‚خپAٹد‘ھ‚إ‚«‚éژ–ڈغگ”‚ح‚ي‚¸‚©‚Qپ“‚ة‚ب‚邱‚ئ‚ة’چ–عپB
(ƒE) —zژqپE—zژqڈص“ث‚ج‘S’f–تگد‚حچ‚ƒGƒlƒ‹ƒMپ[‚إ‚ح~40mb‚إ‚ ‚éپB‚±‚جƒGƒlƒ‹ƒMپ[‚إ‚ج—zژq‚ج”¼Œa‚ح‚¢‚‚ç‚©پHپi”z“_‚Pپj
s»p(r+r)2=4 p r2‚جٹضŒW‚و‚èپA
40mb=40پL10-3پL10-24cm2=4 p r2
r=5.6پL10-14 cmپB—zژq‚ج‘ه‚«‚³‚ح‘ه‘ج10-13 cm’ِ“x‚إ‚ ‚éپB
(ƒG) ƒjƒ…پ[ƒgƒٹƒmپE—zژqڈص“ث‚ج‘S’f–تگد‚ح1GeVƒGƒlƒ‹ƒMپ[—جˆو‚إ~10-36cm2‚إ‚ ‚éپBڈم‚ج—zژq‚ج‘ه‚«‚³‚ًژg‚¤‚ئƒjƒ…پ[ƒgƒٹƒm‚ج‘ه‚«‚³‚ح‚ا‚ج’ِ“x‚ة‚ب‚é‚©پH‚½‚¾‚µپAƒjƒ…پ[ƒgƒٹƒm‚ح‘f—±ژq‚إ‘ه‚«‚³‚ً‚à‚½‚¸پA‚±‚جڈ¬‚³‚بڈص“ث’f–تگد‚حƒjƒ…پ[ƒgƒٹƒmپE—zژqٹش‚ج‘ٹŒفچى—p‚ھڈ¬‚³‚¢‚±‚ئ‚ة‹Nˆِ‚µ‚ؤ‚¢‚éپBپi”z“_‚Pپj
پ– پ–پ–‚±‚ê‚ح–â‘èگف’è‚ھˆ«‚©‚ء‚½‚ج‚إپAچإڈ‰‚ةژس‚è‚ـ‚·پBپ–پ–پ–
پiƒEپj‚ئ“¯—l‚ة‰ً‚‚ئ
10-36cm2=p( rproton +rneutrino)2 ‚إrproton =5.6پL10-14 cm‚ً“ü‚ê‚é‚ئ
rneutrino =-5.6پL10-14 cm‚ئ‚ب‚蕉‚ج‘ه‚«‚³‚ئ‚ب‚éپB‚±‚ê‚ح•¨—“I‰ًژك‚ئ”½‚·‚éپBƒjƒ…پ[ƒgƒٹƒm‚ً‘ه‚«‚³‚ج–³‚¢“_—±ژq‚ئ‚µ‚ؤ‚àپA—zژq‚ئƒjƒ…پ[ƒgƒٹƒm‚ھڈo‰ï‚¤‚ئ•K‚¸”½‰‚·‚é‚ب‚çپA‚â‚ح‚è’f–تگد‚ح10mb‚ئ‚ب‚è~10-36cm2‚ج’f–تگد‚ًگà–¾‚إ‚«‚ب‚¢پB‚±‚ê‚ًگà–¾‚·‚邽‚ك‚ة‚حƒjƒ…پ[ƒgƒٹƒm‚حژم‚¢‘ٹŒفچى—p‚µ‚©‚µ‚ب‚¢‚ج‚إپA’تڈي—zژq‚ئڈص“ث‚¹‚¸‚ة—zژq‚ً‚·‚蔲‚¯‚é‚ئچl‚¦‚ê‚خ‚آ‚¶‚آ‚ـ‚ھ‚ ‚¤پi’چپFپiƒEپj‚جگف’è‚إ‚ح—zژqپE—zژq‚ح‹‚¢‘ٹŒفچى—p‚ً‚·‚é‚ج‚إ•K‚¸ڈص“ث‚·‚é‚ئ‚µ‚½پjپB‚±‚جژپAƒjƒ…پ[ƒgƒٹƒm‚ئ—zژq‚ج”½‰—¦‚ح10-36/10-26=10-10‚إ100‰Œآ‚ة1Œآ‚ھ—zژq‚ئ”½‰‚·‚邱‚ئ‚ة‚ب‚éپB
(ƒI) 1GeV‚جƒjƒ…پ[ƒgƒٹƒm‚ئ—zژqڈص“ث‚ج‘S’f–تگد10-36cm2‚à‚ئ‚ةگ…’†‚إ‚جƒjƒ…پ[ƒgƒٹƒm‚ج‘ٹŒفچى—p’·‚ً‹پ‚ك‚وپBپi”z“_‚Pپj
l=1/(10-36cm2پL1g/cm3پL6.023پL1023/g
=1.66پL1012cm=16,603,022km
—]’k‚إ‚ ‚é‚ھپA’n‹…‚ج’¼Œa‚ح–ٌ13,000km‚ب‚ج‚إپA’n‹…‚ج–§“x‚ًچl—¶‚µ‚ؤ‚àƒjƒ…پ[ƒgƒٹƒm‚ھ’n‹…‚ً‚·‚蔲‚¯‚ؤ‚¢‚‚±‚ئ‚ھ”»‚éپB
‚±‚ج–â‘è‚إگ…‚جŒ´ژq—ت18پig/molپj‚ًژg‚¤‰ً“ڑ—ل‚ھ–ع‚ة•t‚«‚ـ‚µ‚½پB‚±‚جڈêچ‡پAگ…•ھژq‚جŒآگ”‚حNaŒآپ^mol‚إ‚·‚ھپA“üژث—±ژq‚حٹjژq‚ئژU—گ‚·‚é‚ج‚إپA•W“I‚جٹjژqگ”‚ح18 NaŒآپ^mol‚ئ‚ب‚è‚ـ‚·پB‚و‚ء‚ؤ•ھ•êپA•ھژq‚ج18‚ھ‘إ‚؟ڈء‚µ‚ ‚¢پAڈم‚ج“ڑ‚¦‚ج‚و‚¤‚ة‚ب‚è‚ـ‚·پB
(ƒJ) ƒ‰ƒUƒtƒHپ[ƒhژU—گ‚ة‚¨‚¢‚ؤپA“üژث—±ژq‚ج“d‰×‚ًz1eپAƒGƒlƒ‹ƒMپ[‚ًEپA•W“I—±ژq‚ج“d‰×‚ًZ2e‚µ‚ؤژU—گٹp“xq‚ةژU—گ‚³‚ê‚é’f–تگد‚ح
![]()
‚إ‚ ‚éپBƒ‰ƒUƒtƒHپ[ƒhژU—گ‚ج’f–تگد‚ًŒأ“Tک_‚ً‚à‚ئ‚ةŒvژZ‚¹‚وپBپi”z“_‚Pپj
“dژq‚جŒأ“T”¼Œar0پiºe2/4pe0mec2پj‚ً’è‹`‚µ‚ؤ
![]()
‚ئ•\‚¹‚éپBz1=Z2=1پAr0=2.8181پL10-13cmپA“dژq‚جژ؟—ت‚ًmec2=0.511MeVپA‚جڈêچ‡1MeV‚ج—zژq‚ة‘خ‚µ‚ؤ‚ج”÷•ھژU—گ’f–تگد‚ج‘ه‚«‚³‚حپAq=10پ‹پA90پ‹پA180پ‹‚إٹô‚ç‚ة‚ب‚é‚©پHپi”z“_‚Pپj
ژ®‚ج“±ڈo‚حˆê”ت‚ج“dژ¥‹Cٹw‚ج‹³‰بڈ‘‚ًژQڈئ‚µ‚ؤ‰؛‚³‚¢پB‚½‚¢‚ؤ‚¢‚ج–{‚ةڈo‚ؤ‚¢‚ـ‚·پB
q=10پ‹پFپ@ds/dW= 2.2پL10-23cm2=22 b
q=90پ‹پFپ@ds/dW= 5.2پL10-27cm2=5.2 mb
q=180پ‹پFپ@ds/dW= 1.3پL10-27cm2=1.3 mb
q=10پ‹‚ئq=90پ‹‚إ—§‘جٹp‚ھ1–œ”{‹ك‚ˆل‚¤‚±‚ئ‚ة’چ–عپB‘هٹp“xژU—گ‚ح‚ك‚ء‚½‚ة‹N‚ç‚ب‚¢پB
‘S‘ج‚ة‘خ‚·‚éƒRƒپƒ“ƒgپF
Œ‹چ\ŒvژZƒ~ƒX‚ً‚·‚éگl‚ھ‘½‚¢پBŒvژZ‚حگ³ٹm‚ةپB
‘fپEٹj¥‰F’ˆژہŒ±ٹw‡TƒŒƒ|پ[ƒgپi‰ً“ڑپj
2.
4Œژ25پC5Œژ2“ْپ@پ@چ‡Œv”z“_‚Uپi’چپFŒµ–§‚إ‚ح‚ب‚پAگ¬گر‚جژQچlژ‘—؟’ِ“x‚ةژg‚¤پBپj
(ƒA) Bethe-Bloch‚جژ®پ@پi”z“_‚Pپ~‚Qپj
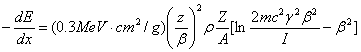
‚إگ…’†‚إ‚ج‰×“d—±ژq‚ج’Pˆت’·‚³‚ ‚½‚è‚ج‹ةڈ¬ƒCƒIƒ“‰»’l‚إ‚جƒGƒlƒ‹ƒMپ[‘¹ژ¸‚ًŒvژZ‚·‚éپBگ…‚جH2O‚ج‚¤‚؟پAژه‚ةO‚ھƒGƒlƒ‹ƒMپ[‘¹ژ¸‚ة—Dگ¨‚¾‚ئ‚µپAI‚ً‹پ‚كڈم‹L‚جژ®‚ة‘م“ü‚µ‹ةڈ¬ƒCƒIƒ“‰»’lپibg=3پj‚إ‚جƒGƒlƒ‹ƒMپ[‘¹ژ¸‚ً‹پ‚ك‚وپB‚ـ‚½”z•zژ‘—؟‚ة‚ ‚éژ_‘f‚جƒCƒIƒ“‰»ƒGƒlƒ‹ƒMپ[‚ًژg‚ء‚½ڈêچ‡‚حƒGƒlƒ‹ƒMپ[‘¹ژ¸‚ح‚ا‚¤‚ب‚é‚©پHژQچl‚ئ‚µ‚ؤ“dژq‚جژ؟—تmc2‚ح511keV‚إ‚ ‚éپB
I پپ16پLZ0.9eV‚جٹضŒWژ®‚و‚èپAI پپ16پL80.9=16پL6.5=104eVپB
bg=b/پم(1-b2پj=3‚جڈêچ‡b=0.95پAg=3.16پB
ڈمژ®‚ة‘م“ü‚·‚é‚ئ
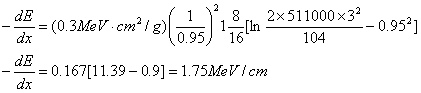
ژQچlژ‘—؟’†‚جژ_‘f‚جƒCƒIƒ“‰»ƒGƒlƒ‹ƒMپ[‚حI پپ16پL80.9=16پL6.5=98.3eVپB
‚±‚جڈêچ‡
![]()
(ƒC) ڈم‹L‚إ‚à‚ئ‚ك‚½‹ةڈ¬ƒCƒIƒ“‰»’l‚ً—p‚¢پA•½‹د‰^“®—ت1GeV/c‚ج‰F’ˆگüƒ~ƒ…پ[ƒIƒ“‚ج‘SƒGƒlƒ‹ƒMپ[پiƒءˆِژq‚ھڈ\•ھ‘ه‚«‚¢‚ج‚إ‰^“x—تپپƒGƒlƒ‹ƒMپ[‚ئ‚µ‚ؤ‚و‚¢پj‚ً‘ھ’è‚·‚邽‚ك‚ة‚حچإ’ل‰½cm‚جƒvƒ‰ƒXƒ`ƒbƒNپiگ…‚ئ“¯‚¶‚إ–§“x‚P.0‚ئ‚·‚éپBپjƒVƒ“ƒ`ƒŒپ[ƒ^‚ھ•K—v‚©پH‚±‚±‚إƒVƒ“ƒ`ƒŒپ[ƒ^‚ئ‚ح‰×“d—±ژq‚ھ“üژث‚·‚é‚ئŒُ‚ً•ْڈo‚·‚镨ژ؟‚ج‚±‚ئ‚إپA‚±‚ج–â‚¢‚ةٹض‚µ‚ؤ‚ح•¨ژ؟‚ً’Pڈƒ‚ةƒvƒ‰ƒXƒ`ƒbƒN‚ئ‚µ‚ؤچl‚¦‚ؤ–â‘è‚ب‚¢پBپi”z“_‚Pپj
1GeVپ€1.75MeV/cm
=1,000MeVپ€1.75eV/cm
=571cm (=5.7m)
‚و‚ء‚ؤچإ’ل571cm‚جƒvƒ‰ƒXƒ`ƒbƒN‚ج‰ٍ‚ھ•K—vپB
(ƒE) ”z•z‚µ‚½ژQچlژ‘—؟‚ً“ا‚فˆب‰؛‚ج–â‚¢‚ة“ڑ‚¦‚وپB‚à‚µٹبŒ‰‚ة‚ـ‚ئ‚ك‚é‚ج‚ھ“‚¯‚ê‚خژQچl•¶Œ£‚ً‚»‚ج‚ـ‚ـ“ْ–{Œê‚ة–َ‚µ‚ؤ‚à‚و‚¢پB
‡@ ‰×“d—±ژq‚جƒGƒlƒ‹ƒMپ[‘¹ژ¸‚ً—تژqک_ژg‚ء‚ؤŒvژZ‚·‚éچغ‚ةپAŒأ“Tک_‚ئ”نٹr‚µ‚ؤ—تژqک_‚ج‚ا‚ج‚و‚¤‚ب“ء’¥‚ًژو‚è“ü‚ê‚ؤ‚¢‚é‚©پHپi”z“_‚Pپj
پi‚Pپj“üژث—±ژq‚©‚猴ژq’†‚ج“dژq‚ض‚جƒGƒlƒ‹ƒMپ[‘Jˆع‚ھ—£ژU“I‚إ‚ ‚邱‚ئپB
پi‚Qپj—±ژq‚ج”g“®گ«
‡A •¨ژ؟‚ج–§“x•âگ³ˆِژq‚ئ‚حپA‚ا‚ج‚و‚¤‚بŒ»ڈغ‚ًژو‚舵‚ء‚ؤ‚¢‚é‚©‚ًگà–¾‚¹‚وپBپi”z“_‚Pپj
‰نپX‚ج‹cک_‚إ‚ح“üژث—±ژq‚ھŒا—§‚µ‚½پi“ئ—§‚µ‚½‘½گ”‚جپjŒ´ژq‚ئ‘ٹŒفچى—p‚·‚é‚ئ‚µ‚ؤ‚«‚½پB‚µ‚©‚µپA•¨ژ؟‚ج–§“x‚ھڈم‚ھ‚é‚ئ‚±‚ج‰¼’è‚حگ³‚µ‚‚ب‚پA“üژث—±ژq‚ح‹–‚³‚ꂽƒCƒ“ƒpƒNƒgƒpƒ‰ƒپپ[ƒ^‚ج”حˆح“à‚إ‘½گ”‚جŒ´ژq‚ئ‘ٹŒفچى—p‚·‚邱‚ئ‚ة‚ب‚éپB‚±‚جڈêچ‡پA‘½گ”‚جŒ´ژq’†‚ة‘¶چف‚·‚é“dژq‚حپA“üژث—±ژq‚ئ•W“I“dژq‚ئ‚جٹش‚ج“dڈê‚ة‘خ‚µ‚ؤژص•ءŒّ‰تپiScreening effectپj‚ً‹N‚±‚µپAژہچغ‚ةٹ´‚¶‚é“dڈê‚ھژہŒّ“I‚ة‚حڈ¬‚³‚‚ب‚ء‚ؤ‚µ‚ـ‚¤پB‚»‚µ‚ؤ‹——£‚ً’u‚¢‚½“dژq‚ئ‚ج‘ٹŒفچى—p‚ة‚و‚éƒGƒlƒ‹ƒMپ[‘¹ژ¸‚حڈ¬‚³‚‚ب‚éپB–§“xŒّ‰ت‚ًچl—¶‚·‚é‚ئپAƒGƒlƒ‹ƒMپ[‘¹ژ¸‚ج‘ٹ‘خک_“Iڈمڈ¸‚ھ–³Œہ‚ة‘±‚‚±‚ئ‚حژہچغ‚ة–³‚¢پB
‡B Œ´ژqٹj‚جƒVƒFƒ‹•âگ³C‚جŒّ‰ت‚ح‰×“d—±ژq‚ج‘¬“x‚ھ‘¬‚¢ژ‚ةŒ»‚ê‚éŒّ‰ت‚©‚à‚µ‚‚ح’x‚¢ژ‚ةŒ»‚ê‚éŒّ‰ت‚©پH‚ـ‚½‚±‚ج‚±‚ئ‚ً’¼ٹ´“I‚ة‚ح‚ا‚¤گà–¾‚·‚ê‚خ‚و‚¢‚©پHپi”z“_‚Pپj
Œ´ژqٹj‚جƒVƒFƒ‹•âگ³Œّ‰ت‚ح“üژث—±ژq‚ج‘¬“x‚ھ’x‚¢ژ‚ةŒ°’ک‚ة‚ب‚éپB’¼ٹ´“I‚بگà–¾‚حˆب‰؛‚ةڈq‚ׂéپB“üژث—±ژq‚ج‘¬“x‚ھ’x‚¢‚ئپA“üژث—±ژq‚ئ•W“I“dژq‚ج‘ٹŒفچى—p‚µ‚ؤ‚¢‚éژٹش‚ھ’·‚‚ب‚éپB‚±‚جژٹش‚ھ’·‚¢‚ئ“dژq‚ھŒ´ژqٹj‚جژü‚è‚ً‰^“®‚·‚é‚ج‚ةڈ\•ھ‚بژٹش‚ھ‚ ‚èپA“dژq‚حژ©—R—±ژq‚ئ‚حگU•‘‚ي‚¸پAŒ´ژqٹj‚ة‘©”›‚³‚ê‚ؤ‚½‚à‚ج‚ئ‚µ‚ؤگU•‘‚¤پB‚±‚ج‚و‚¤‚ةŒ´ژqٹj‚ة‘©”›‚³‚ꂽ“dژq‚ئژ©—R“dژq‚ئ‚جˆل‚¢‚ھƒVƒFƒ‹•âگ³ˆِژqC‚ئ‚µ‚ؤ•âگ³‚³‚ê‚éپB
’ٌڈo’÷‚كگط‚èپF5Œژ16“ْ(‹à)ژِ‹ئ‚جژ‚ـ‚إپI
‘fپEٹj¥‰F’ˆژہŒ±ٹw‡TƒŒƒ|پ[ƒgپi‰ً“ڑپj
3.
5Œژ16پA23پA30“ْچ‡Œv”z“_5پi’چپFŒµ–§‚إ‚ح‚ب‚پAگ¬گر‚جژQچlژ‘—؟’ِ“x‚ةژg‚¤پBپj
(ƒA)
پ@‰×“d—±ژq‚جƒGƒlƒ‹ƒMپ[‘ھ’è‚ج‰—p‚جˆê‚آ‚حپAŒںڈoٹي’†‚إ‚جdE/dx‚ً‘ھ’肵پA—±ژq‚ج“¯’è‚ًچs‚¤‚±‚ئ‚إ‚ ‚éپBƒAƒ‹ƒSƒ“(Ar)‚ج‹l‚ـ‚ء‚½”ن—لŒvگ”ٹا’†‚ًƒGƒlƒ‹ƒMپ[300MeV‚ج‰×“dƒخ’†ٹشژqپiژ؟—ت140MeV/c2پjپj‚ھ’ت‰ك‚·‚éژ‚ئ—zژqپiژ؟—ت938MeV/c2پj‚ھ’ت‰ك‚·‚éژ‚جƒGƒlƒ‹ƒMپ[‘¹ژ¸‚ً‚»‚ꂼ‚ê‹پ‚ك‚وپBArپiŒ´ژq”شچ†18پAژ؟—تگ”40پj‚ج–§“x‚ح1.78g/l‚ئ‚·‚éپBƒGƒlƒ‹ƒMپ[‘¹ژ¸‚جŒvژZ‚ة‚حBethe-Bloch‚جژ®
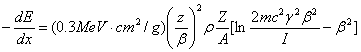
‚ً—p‚¢‚وپBپi”z“_‚Pپj
‚±‚ج–â‘è‚إپAƒGƒlƒ‹ƒMپ[‚ج’è‹`‚ھ‚ ‚¢‚ـ‚¢‚إگ\‚µ–َ‚ ‚è‚ـ‚¹‚ٌ‚إ‚µ‚½پB—zژq‚جƒGƒlƒ‹ƒMپ[‚ً300MeVپiژ؟—تƒGƒlƒ‹ƒMپ[‚و‚èڈ¬‚³‚¢پj‚ئ‚µ‚ؤ‚¢‚é‚و‚¤‚ةپA‰^“®ƒGƒlƒ‹ƒMپ[پi‘SƒGƒlƒ‹ƒMپ[‚©‚ç—±ژq‚جژ؟—ت•ھ‚ًچ·‚µˆّ‚¢‚½•ھپj‚ًچl‚¦‚ؤ‚¢‚ـ‚·پB
‚ـ‚½پA”ٌڈي‚ة‘½‚‚جگl‚ھڈمژ®‚جmc2‚ةƒخ’†ٹشژqپA—zژq‚جژ؟—ت‚ً‘م“ü‚µ‚ؤ‚¢‚ـ‚µ‚½‚ھپA‚±‚ê‚ح•W“I‘¤‚ج“dژq‚جژ؟—ت‚إ‚·پB
‰ٌ“ڑ‚إ‚·پB
I پپ16پLZ0.9eV‚جٹضŒWژ®‚و‚èپAI پپ16پL180.9=215.7eVپB
g=E/m=(140+300)/140=3.14‚©‚瓱ڈo‚µ‚ؤپAbg=p/m=417/140=2.98پAb=0.948پB
‚ـ‚½•ت‚ج‹پ‚ك•û‚ئ‚µ‚ؤ‚ح‰^“®ƒGƒlƒ‹ƒMپ[‚ًE0پA’تڈي‚ج‘SƒGƒlƒ‹ƒMپ[‚ًE‚ئ‚µ‚ؤپAE0ºE-m‚ئ‚·‚é‚ئپA
E2=(E0+m)2پA
E2=E02+2mE0+m2
‰^“®—ت‚حp2= E02+2mE0‚©‚çپAbپAg‚ً‹پ‚ك‚ؤ‚à‚و‚¢پB‰×“dð’†ٹشژq‚جƒGƒlƒ‹ƒMپ[‚ھ300MeV‚جڈêچ‡پA‰^“®—ت‚ح417MeV/cپB
![]() -dE/dx=2.61keV/cm
-dE/dx=2.61keV/cm
—zژq‚جƒGƒlƒ‹ƒMپ[‚ھ300MeV‚جڈêچ‡پAg=E/m=(938+300)/938=1.32‚©‚çbg=p/m=808/938=0.861پAb=0.652پA‰^“®—ت‚ح808MeV/cپB
![]() -dE/dx=4.37keV/cm
-dE/dx=4.37keV/cm
—zژq‚ئƒخ’†ٹشژq‚ھ“¯‚¶ƒGƒlƒ‹ƒMپ[‚ًژ‚آڈêچ‡‚إ‚àپA‚»‚جژ؟—ت‚جˆل‚¢‚ة‚و‚è’Pˆت’·‚³‚ ‚½‚è‚جƒGƒlƒ‹ƒMپ[‘¹ژ¸‚ھˆظ‚ب‚èپA‚»‚ê‚ً‘ھ’è‚·‚邱‚ئ‚إ—zژq‚ئƒخ’†ٹشژq‚ًژ¯•ت‚·‚邱‚ئ‚ھ‰آ”\‚إ‚·پB
‚ـ‚½پAچ،‰ٌ‚حƒGƒlƒ‹ƒMپ[‚ج’è‹`‚ھB–†‚¾‚ء‚½‚½‚كپAƒGƒlƒ‹ƒMپ[پپ‰^“®—ت‚ئ’u‚«ٹ·‚¦‚ؤ‰ٌ“ڑ‚µ‚½گl‚àگ³‰ً‚ئ‚µ‚ـ‚·پB
‰×“dp’†ٹشژq‚ج‰^“®—ت‚ھ300MeV‚جڈêچ‡پAbg=p/m=300/140=2.143پAb=0.906
![]() -dE/dx=2.68keV/cm
-dE/dx=2.68keV/cm
—zژq‚ج‰^“®—ت‚ھ300MeV‚جڈêچ‡پAbg=p/m=300/938=0.320پAb=0.305
![]() -dE/dx=15.7keV/cm
-dE/dx=15.7keV/cm
(ƒC)
پ@ƒVƒ“ƒ`ƒŒپ[ƒ^Œںڈoٹي‚ج‰—p‚جˆê‚آ‚حپA‚»‚ج‘¬‚¢ژٹش‰“ڑ‚ًژ‚ء‚ؤپi‘¬‚¢ƒVƒ“ƒ`ƒŒپ[ƒ^Œںڈoٹي‚إژٹش•ھ‰ً”\0.1n•bپj‰×“d—±ژq‚ج’ت‰كژٹشپiTOFپFTime of Flightپj‚ً‘ھ’è‚ً‚µپA—±ژq‚ج“¯’è‚ًچs‚¤‚±‚ئ‚إ‚ ‚éپBƒVƒ“ƒ`ƒŒپ[ƒ^2–‡‚ً3m‚جٹشٹu‚ً—£‚µ‚ؤ’u‚«پA300MeV‚جƒGƒlƒ‹ƒMپ[‚ج—z“dژqپiژ؟—ت0.511MeV/c2پjپA‰×“dƒخ’†ٹشژqپA—zژq‚ً’ت‰ك‚³‚¹‚éپB‚»‚ꂼ‚ê‚ج—±ژq‚ھƒVƒ“ƒ`ƒŒپ[ƒ^ٹش‚ً’ت‰ك‚·‚é‚ج‚ة—v‚·‚éژٹش‚ًŒvژZ‚¹‚وپB‚±‚جŒvژZŒ‹‰ت‚©‚çپA“¯ˆê‰^“®—ت‚ج‰×“d—±ژq‚ًTOF–@‚ة‚و‚ء‚ؤپA—±ژq“¯’è‚ھ‰آ”\‚إ‚ ‚éژ–‚ھ—‰ً‚إ‚«‚éپBپi”z“_‚Pپj
–â‘èپiƒAپj‚ئ“¯—l‚إ‚·پB
‘O–â‚و‚èپA—zژqپA‰×“dƒpƒC’†ٹشژq‚ج‘¬“x‚ح‚»‚ꂼ‚êƒہپپ0.652پA0.948پD
—z“dژq‚ةٹض‚µ‚ؤ‚ح
ƒGƒlƒ‹ƒMپ[‚ھ300MeV‚جڈêچ‡پA‰^“®—ت‚ح300.5@300MeV/c‚ب‚ج‚إ
bg=p/m=300/0.511=587.1پAb=0.9999985@1.0
ٹe—±ژq‚ھ3m‚جٹشٹu‚ً’ت‰ك‚·‚éژٹش‚حپAŒُ‘¬3پL108m/s(=0.3m/ns)‚ًچl—¶‚µ‚ؤ(ns=ƒiƒm•b)
—zژqپFپ@3¸(0.3پL0.652) = 15.3 nsec
ƒخ’†ٹشژqپF 3¸(0.3پL0.948) = 10.5 nsec
—z“dژqپF3¸(0.3پL1) = 10 nsec
‚و‚ء‚ؤپA0.5nsec‚جگ¸“xˆبڈم‚إژٹش‘ھ’è‚ھ‚إ‚«‚ê‚خپA—zژqپAƒpƒC’†ٹشژqپA—z“dژq‚جژ¯•ت‚ھچs‚¦‚éپBژہچغ‚جTOFƒVƒXƒeƒ€‚إ‚ح0.1nsec’ِ“x‚جژٹش•ھ‰ً”\‚ھ‚ ‚é‚ج‚إپA—zژqپAƒpƒC’†ٹشژqپA—z“dژq‚جژ¯•ت‚حڈ\•ھ‰آ”\‚إ‚ ‚éپB
ƒGƒlƒ‹ƒMپ[پپ‰^“®—ت‚ئ‰¼’肵‚½گl‚حپA—zژqپA‰×“dƒpƒC’†ٹشژq‚ج‘¬“x‚ح‚»‚ꂼ‚êƒہپپ0.305پA0.906پD—z“dژq‚ةٹض‚µ‚ؤ‚ح
bg=p/m=300/0.511=587.1پAb=0.9999985@1.0
ٹe—±ژq‚ھ3m‚جٹشٹu‚ً’ت‰ك‚·‚éژٹش‚حپAŒُ‘¬3پL108m/s(=0.3m/ns)‚ًچl—¶‚µ‚ؤ(ns=ƒiƒm•b)
—zژqپFپ@3¸(0.3پL0.305) = 32.8 nsec
ƒخ’†ٹشژqپF 3¸(0.3پL0.906) = 11.04 nsec
—z“dژqپF3¸(0.3پL1) = 10 nsec
‚و‚ء‚ؤپA0.1nsec‚جگ¸“xˆبڈم‚إژٹش‘ھ’è‚ھ‚إ‚«‚ê‚خپA—zژqپAƒpƒC’†ٹشژqپA—z“dژq‚جژ¯•ت‚ھچs‚¦‚éپB
(ƒE)
پ@ƒVƒ“ƒ`ƒŒپ[ƒ^‚جŒُ—تپB
NaI(Tl)ƒVƒ“ƒ`ƒŒپ[ƒ^‚ح‚PMeV‚جŒُژq‚ة‘خ‚µ‚ؤ–ٌ40,000Œآ‚جŒُژq‚ً•ْڈo‚·‚éپBژg—p‚·‚éŒُ“dژq‘”{ٹا‚ج—تژqŒّ—¦‚ً20پ“‚ئ‚µ‚ؤپANaI(Tl)‚©‚ç‚جŒُ‚ج“à10پ“‚ًژûڈW‚إ‚«‚é‚ئ‰¼’肵‚½ڈêچ‡پA‰½Œآ‚جŒُ“dژq‚ھŒُ“dژq‘”{ٹا‚إŒv‘ھ‚³‚ê‚é‚©پH‚ـ‚½پAŒُ“dژqگ”‚ج‚ن‚炬پi•Wڈ€•خچ·ƒذپj‚حƒKƒEƒX•ھ•z‚ةڈ]‚¤‚ئ‰¼’肵پANaI(Tl)‚ج‚PMeV‚جŒُژq‚ة‘خ‚·‚éƒGƒlƒ‹ƒMپ[•ھ‰ً”\‚ًŒ©گد‚à‚è‚ب‚³‚¢پH•½‹دNŒآ‚ً’†گS‚ئ‚·‚éƒKƒEƒX•ھ•z‚ج•Wڈ€•خچ·‚ح![]() ‚ئ‚ب‚éپB‚ـ‚½ƒGƒlƒ‹ƒMپ[•ھ‰ً”\‚ح
‚ئ‚ب‚éپB‚ـ‚½ƒGƒlƒ‹ƒMپ[•ھ‰ً”\‚ح
پiƒGƒlƒ‹ƒMپ[‚ج—h‚炬‚آ‚ـ‚è•Wڈ€•خچ·پjپ^پiٹد‘ھ‚³‚ꂽƒGƒlƒ‹ƒMپ[‚ج•½‹د’lپj
‚ئ‚µ‚ؤ’è‹`‚³‚ê‚ـ‚·پBپi”z“_‚Pپj
‰½گl‚©‚جگl‚ھٹ¨ˆل‚¢‚µ‚ؤ‚¢‚ـ‚µ‚½‚ھپAŒُ“dژq‚حŒُ“dژq‘”{ٹا‚جŒُ“d‰A‹ة‚©‚çڈo‚ؤ‚‚é“dژq‚إ‚·پB‚و‚ء‚ؤŒُ“dژqگ”‚حŒُ“d‰A‹ة‚©‚çڈo‚ؤ‚‚é“dژq‚جŒآگ”‚إŒُ“dژq‘”{ٹا‚ج‘•—¦‚ئ‚حٹضŒW‚ ‚è‚ـ‚¹‚ٌپB
40,000پL0.2پL0.1=800Œآ‚ج“dژq‚ھٹد‘ھ‚³‚ê‚éپB
‚»‚جژ‚جŒُ“dژqگ”‚ج—h‚炬‚حپم800=28.3Œآ‚إ‚ ‚éپB
‚و‚ء‚ؤپA—\‘z‚³‚ê‚éƒGƒlƒ‹ƒMپ[•ھ‰ً”\‚ح28.3پ€800=0.035پB
3.5پ“’ِ“x‚جƒGƒlƒ‹ƒMپ[•ھ‰ً”\‚ھٹْ‘ز‚³‚ê‚éپB
(ƒG)
پ@137Cs‚©‚ç‚ج662keV‚جƒKƒ“ƒ}پ[گü‚ھƒRƒ“ƒvƒgƒ“ژU—گ‚ة‚و‚èŒںڈoٹي‚إ90“x•ûŒü‚ةژU—گ‚³‚ꂽڈêچ‡پA‰½keV‚جƒGƒlƒ‹ƒMپ[‚ھŒںڈoٹي‚إٹد‘ھ‚³‚ê‚é‚©‹پ‚ك‚وپH‚ـ‚½‚±‚ج662keV‚جƒءگü‚ھ1‰ٌ‚جƒRƒ“ƒvƒgƒ“ژU—گ‚إŒںڈoٹي’†‚ة—ژ‚ئ‚·چإ‘هƒGƒlƒ‹ƒMپ[‚حٹô‚ç‚©ŒvژZ‚µ‚ب‚³‚¢پHچإ‘هƒGƒlƒ‹ƒMپ[‚ً—ژ‚ئ‚·ڈêچ‡پAƒءگü‚ح‚ا‚ج•ûŒü‚ةژU—گ‚³‚ê‚ؤ‚¢‚é‚©‚à‹پ‚ك‚وپHپi”z“_‚Pپj
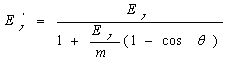
‚ب‚ج‚إژU—گŒم‚جƒءگü‚جƒGƒlƒ‹ƒMپ[‚ح
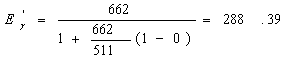
Œںڈoٹي‚إٹد‘ھ‚³‚ê‚é‚ج‚حژU—گ‚³‚ꂽ“dژq‚ج‰^“®ƒGƒlƒ‹ƒMپ[‚ب‚ج‚إ
662پ|288.4پپ373.6keVپB
‚±‚±‚إپA“dژq‚حڈء–إ‚µ‚ب‚¢‚ج‚إپA“dژq‚ج‘SƒGƒlƒ‹ƒMپ[پiگأژ~ژ؟—ت‚ً‰ءژZ‚µ‚½‚à‚جپj‚ًژg‚¤‚ئٹشˆل‚ء‚½“ڑ‚¦‚ئ‚ب‚éپB‚ـ‚½Œںڈoٹي‚إٹد‘ھ‚³‚ê‚éƒGƒlƒ‹ƒMپ[‚ًگq‚ث‚ؤ‚¢‚é‚ج‚ةپAژU—گ‚³‚ꂽŒُژq‚جƒGƒlƒ‹ƒMپ[‚ً“ڑ‚¦‚½گl‚ھ‘½‚©‚ء‚½پB
Œںڈoٹي‚ةچإ‘هƒGƒlƒ‹ƒMپ[‚ھ—ژ‚؟‚é‚ج‚حپAژU—گƒءگü‚جƒGƒlƒ‹ƒMپ[‚ھچإڈ¬‚جژ‚إ‚ ‚éپBڈم‹L‚جژ®‚و‚èƒئپپ180پ‹‚جژ‚ب‚ج‚إپAڈم‹L‚جژ®‚ة‘م“ü‚µ
Egپf=184keV, Ee=662-184=478MeVپB
‚±‚جŒںڈoٹي’†‚إƒRƒ“ƒvƒgƒ“ژU—گ‚إ—ژ‚ئ‚³‚ê‚éچإ‘هƒGƒlƒ‹ƒMپ[‚ھƒRƒ“ƒvƒgƒ“ƒGƒbƒW‚إ‚ ‚éپB
(ƒI)
60Co‚حˆê“x‚ج•ِ‰َ‚إ1.17MeV‚ئ1.33MeV‚ج2–{‚جƒءگü‚ً•ْڈo‚µ‚ـ‚·پB1MBqپiƒپƒKƒxƒNƒŒƒ‹پj‚ج‹“x‚ج60CoگüŒ¹‚ج‰”‚ة‚و‚éژص•ء‚ًچl‚¦‚ـ‚·پB‰”’†‚ج–ٌ‚PMeVپi1.17MeV‚ئ1.33MeV‚à“¯—lپj‚جŒُژq‚جŒ¸گٹ’·‚ح2cm‚إ‚ ‚éپB1MBq‚ج60CoگüŒ¹‚©‚çڈo‚ؤ‚‚éƒءگü‚جگü—ت‚ھ1Œآپ^•bˆب‰؛‚ة‚·‚邽‚ك‚ة‚ح‰½cmŒْ‚ج‰”‚إگüŒ¹‚ًˆح‚¤•K—v‚ھ‚ ‚é‚©ŒvژZ‚µ‚ب‚³‚¢پB‚±‚±‚إ60Co‚©‚ç‚حˆê“x‚ج•ِ‰َ‚إƒءگü‚ھ2Œآ•ْڈo‚³‚ê‚邱‚ئ‚ة’چˆس‚·‚邱‚ئپBپi”z“_‚Pپj
60Co‚ح1‰ٌ‚ج•ِ‰َ‚إ2Œآ‚ج•ْژثگü‚ً•ْڈo‚·‚é‚ج‚إپA‚PMB‚‘‚جگüŒ¹‚إ2000,000Œآ‚ج•ْژثگü‚ً•ْڈo‚·‚éپB•K—v‚ب‰”‚جŒْ‚³‚ًxcm‚ئ‚·‚é‚ئ
2000,000پ~exp(-x/2)=1
x=29.017cm
‚و‚ء‚ؤپA–ˆ•b1Œآ‚جƒءگü‚µ‚©‹–‚³‚ب‚¢‚ئ‚·‚é‚ئگüŒ¹‚ً29cmŒْ‚ج‰”‚إ•¢‚¤•K—v‚ھ‚ ‚éپB
’ٌڈo’÷‚كگط‚èپF6Œژ13“ْ(‹à)ژِ‹ئ‚جژ‚ـ‚إپI