素・核･宇宙実験学�Tレポート

1. 4月11，18日

(ア) 陽子の重さは何kgか？

(イ) 標的から10cmのところに表面積25cm²のNaIシンチレーター検出器を設置した。標的を臨む立体角はいくらか？また標的から粒子が等方的に散乱されているとすると、全体の何％の粒子が検出器で観測されるか？

(ウ) 陽子・陽子衝突の全断面積は高エネルギーでは~40mbである。このエネルギーでの陽子の半径はいくらか？

(エ) ニュートリノ・陽子衝突の全断面積は1GeVエネルギー領域で~10^-36cm²である。上の陽子の大きさを使うとニュートリノの大きさはどの程度になるか？ただし、ニュートリノは素粒子で大きさをもたず、この小さな衝突断面積はニュートリノ・陽子間の相互作用が小さいことに起因している。

(オ) 1GeVのニュートリノと陽子衝突の全断面積10^-36cm²もとに水中でのニュートリノの相互作用長を求めよ。

(カ) ラザフォード散乱において、入射粒子の電荷をz₁e、エネルギーをE、標的粒子の電荷をZ₂eして散乱角度qに散乱される断面積は

である。ラザフォード散乱の断面積を古典論をもとに計算せよ。

電子の古典半径r₀（ºe²/4pe₀m_ec²）を定義して

と表せる。z₁=Z₂=1、r₀=2.8181´10^-13cm、電子の質量をm_ec²=0.511MeV、の場合1MeVの陽子に対しての微分散乱断面積の大きさは、q=10°、90°、180°で幾らになるか？

(キ) 講義に関する要請・コメント等あれば書いて下さい。

提出締め切り：5月2日(金)授業の時まで！

素・核･宇宙実験学�Tレポート

2. 4月25，5月2日

(ア) Bethe-Blochの式

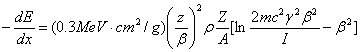
で水中での荷電粒子の単位長さあたりの極小イオン化値でのエネルギー損失を計算する。水のH₂Oのうち、主にOがエネルギー損失に優勢だとし、Iを求め上記の式に代入し極小イオン化値（bg=3）でのエネルギー損失を求めよ。また配布資料にある酸素のイオン化エネルギーを使った場合はエネルギー損失はどうなるか？参考として電子の質量mc²は511keVである。

(イ) 上記でもとめた極小イオン化値を用い、平均運動量1GeV/cの宇宙線ミューオンの全エネルギー（γ因子が十分大きいので運度量＝エネルギーとしてよい）を測定するためには最低何cmのプラスチック（水と同じで密度１.0とする。）シンチレータが必要か？ここでシンチレータとは荷電粒子が入射すると光を放出する物質のことで、この問いに関しては物質を単純にプラスチックとして考えて問題ない。

(ウ) 配布した参考資料を読み以下の問いに答えよ。もし簡潔にまとめるのが難しければ参考文献をそのまま日本語に訳してもよい。

�@ 荷電粒子のエネルギー損失を量子論使って計算する際に、古典論と比較して量子論のどのような特徴を取り入れているか？

�A 物質の密度補正因子とは、どのような現象を取り扱っているかを説明せよ。

�B 原子核のシェル補正Cの効果は荷電粒子の速度が速い時に現れる効果かもしくは遅い時に現れる効果か？またこのことを直感的にはどう説明すればよいか？

提出締め切り：5月16日(金)授業の時まで！

素・核･宇宙実験学�Tレポート

3. 5月16、23、30日

(ア) 　荷電粒子のエネルギー測定の応用の一つは、検出器中でのdE/dxを測定し、粒子の同定を行うことである。アルゴン(Ar)の詰まった比例計数管中をエネルギー300MeVの荷電π中間子（質量140MeV/c²））が通過する時と陽子（質量938MeV/c²）が通過する時のエネルギー損失をそれぞれ求めよ。Ar（原子番号18、質量数40）の密度は1.78g/lとする。エネルギー損失の計算にはBethe-Blochの式

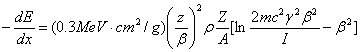
を用いよ。

(イ) 　シンチレータ検出器の応用の一つは、その速い時間応答を持って（速いシンチレータ検出器で時間分解能0.1n秒）荷電粒子の通過時間（TOF：Time of Flight）を測定をし、粒子の同定を行うことである。シンチレータ2枚を3mの間隔を離して置き、300MeVのエネルギーの陽電子（質量0.511MeV/c²）、荷電π中間子、陽子を通過させる。それぞれの粒子がシンチレータ間を通過するのに要する時間を計算せよ。この計算結果から、同一運動量の荷電粒子をTOF法によって、粒子同定が可能である事が理解できる。

(ウ) 　シンチレータの光量。

NaI(Tl)シンチレータは１MeVの光子に対して約40,000個の光子を放出する。使用する光電子増倍管の量子効率を20％として、NaI(Tl)からの光の内10％を収集できると仮定した場合、何個の光電子が光電子増倍管で計測されるか？また、光電子数のゆらぎ（標準偏差σ）はガウス分布に従うと仮定し、NaI(Tl)の１MeVの光子に対するエネルギー分解能を見積もりなさい？平均N個を中心とするガウス分布の標準偏差はとなる。またエネルギー分解能は

（エネルギーの揺らぎつまり標準偏差）／（観測されたエネルギーの平均値）

として定義されます。

(エ) 　¹³⁷Csからの662keVのガンマー線がコンプトン散乱により検出器で90度方向に散乱された場合、何keVのエネルギーが検出器で観測されるか求めよ？またこの662keVのγ線が1回のコンプトン散乱で検出器中に落とす最大エネルギーは幾らか計算しなさい？最大エネルギーを落とす場合、γ線はどの方向に散乱されているかも求めよ？

(オ) ⁶⁰Coは一度の崩壊で1.17MeVと1.33MeVの2本のγ線を放出します。1MBq（メガベクレル）の強度の⁶⁰Co線源の鉛による遮蔽を考えます。鉛中の約１MeV（1.17MeVと1.33MeVも同様）の光子の減衰長は2cmである。1MBqの⁶⁰Co線源から出てくるγ線の線量が1個／秒以下にするためには何cm厚の鉛で線源を囲う必要があるか計算しなさい。ここで⁶⁰Coからは一度の崩壊でγ線が2個放出されることに注意すること。

提出締め切り：6月13日(金)授業の時まで！